FAC - Aula 03: Número de elementos de um conjunto

Módulo 01 - Conjunto

Conteúdo:

1. Conceitos iniciais
2. Introdução ao princípio aditivo
3. Introdução ao princípio da inclusão e exclusão
4. Questões de AD´s e AP´s do Cederj
5. Bibliografia

1. Conceitos iniciais

O uso da "sigma"

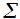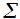Apesar de não constar no conteúdo dessa aula nas transparências do Cederj é importante compreendermos daqui para frente o uso do símbolo , que é uma letra gregra na matemática muito utilizada chamada sigma, e que deveria ser aprendido no 2º grau, mas muitas pessoas não sabem como utilizar. Essa letra simboliza as somatórias. Vamos a um exemplo:

Assim, essa representação indica a soma dos números obtidos na expressão 2i, conforme substituímos i por 1, 2, 3, 4 e 5.

i = 1 2i = 2
i = 2 2i = 4
i = 3 2i = 6
i = 4 2i = 8
i = 5 2i = 10



Notação

Formar conjunto é contar seu número de elementos e para isso precisamos desenvolver a noção de contagem. Para solucionarmos muitos problemas as vezes consiste somente em contar o numero de elementos de um certo conjunto. Por exemplo, contar o número de elementos de uma equação ou de um problema.

Para isso utilizamos a seguinte notação

= número de elementos do conjunto A (ou cardinalidade de A).

Exemplo 1:

A = { x | |x| 2 } = { x | - 2 x 2 }
= { -2, -1, 0, 1, 2 }

= 5

Para solucionar esse exemplo fizemos:

1 é o número -2
2 é o número -1
3 é o número 0
4 é o número 1
5 é o número 2

Resolução igual a 5 elementos

Exemplo 2:

Mas se tivessemos que inumerar o número de elementos do conjunto:

B = { x | x é ímpar }
= { 1, 3, 5, 7 ... }

Neste caso podemos ir enumerando seus elementos mas nunca acabaremos a enumeração, logo uma resposta pode ser dada; nem sempre podemos acabar a enumeração de um conjunto.

Definição de conjuntos finito e infinito

Para estabelecer se um conjunto é finito ou infinito vamos usar a noção de bijeção, isto é, uma função f: X Y entre dois conjuntos X e Y tal que:

• Se a e b são elementos de X tais que f (a) = f (b), então a = b. Dito de outra maneira, se f (a) f (b), então a b.

• Para todo elemento b Y, existe algum elemento de a X tal que f (a) = b.

Logo, uma bijeção entre dois conjuntos estabelece uma relação um a um entre os seus elementos.

Exemplo 01:

A função f: { 1, 2, 3, 4, 5, 6, ... } { 2, 4, 6, 8, 10, 12, ... }, definido por f (x) = 2x, é uma bijeção entre o conjunto dos números naturais e o conjunto dos números pares.

Então podemos dizer que um conjunto X é infinito se existe um subconjunto próprio Y ? X e uma bijeção f: X Y.

O exemplo mostra que o conjunto dos números naturais é infinito. Com isso, quando um conjunto não é infinito ele é chamado de finito.

Parece estranho e simples, iniciar pelo infinito, e definir dessa forma que é mais complicado.

Então podemos pensar porque simplesmente não contamos o número dos elementos? O importante que devemos entender é que contar é uma aplicação da noção de bijeção. Se entendermos a noção de bijeção podemos comparar conjuntos sem, necessariamente, contar o número de seus elementos.

Ao contarmos o número de elementos de um conjunto finito, estamos criando uma bijeção entre ele e o conjunto { 1, 2, 3, 4, ..., n }, onde n é o seu número de elementos.

No entanto, na prática, podemos não conseguir realizar uma contagem de elementos de um conjunto. Exemplo; qual o número de estrelas na nossa galáxia?

O conjunto contrário ao finito é chamado de infinito. Os conjuntos dos números inteiros positivos, conjunto dos números reais e o conjunto de palavras que podemos formar com nosso alfabeto, são exemplos de conjuntos infinitos.

Observação: O conjunto vazio não tem elementos, logo n () = 0.

2. Introdução ao princípio aditivo

Como encontrar uma fórmula para calcular n ( A ∪ B )?

Princípio aditivo para dois conjuntos

Para dois conjuntos podemos considerar se A B e são disjuntos A B = , então n (A ∪ B) = n (A) + n (B).

Exemplo 1:

Sejam A = { 1, 2, 3 } e B = { 4, 5, 6 }. Então:

n (A) = 3

n (B) = 3

n (A ∪ B) = 6

n (A B) = 0

Se A e B são dois conjuntos disjuntos, então n (A ∪ B) = n (A) + n (B), pois se x A ∪ B então x A ou x B, mas x não pode estar em ambos A e B, já que A B = .

No exemplo, temos que n ( A ∪ B) = 6, ou seja n ( A ) + n ( B ) = 3 + 3 = 6.

Princípio aditivo para três conjuntos

E se fosse três conjunto?

Sejam A = { 1, 2, 3 } , B = { 4, 5, 6 } e C = { 7, 8, 9, 10 }

Então teríamos A, B e C, que são disjuntos dois a dois:

A B =
A C =
B C =

Logo, n ( A ∪ B ∪ C ) = n ( A ) + n ( B ) + n ( C )

n ( A ) = 3
n ( B ) = 3
n ( C ) = 4
n ( A ∪ B ∪ C ) = 10

Prova:

n ( A ∪ B ∪ C ) = n (( A ∪ B) ∪ C ) =

???

Princípio aditivo para quatro conjuntos

????

3. Introdução ao princípio da inclusão e exclusão
Princípio da inclusão e exclusão para dois conjuntos

Se A e B são dois conjuntos finitos, então

n ( A ∪ B ) = n ( A ) + n ( B ) - n ( A B )

Para entendermos, observe o diagrama a seguir, onde vemos que A ∪ B pode ser visto como a união de três conjuntos disjuntos:

A ∪ B = ( A - B ) ∪ ( A B ) ∪ ( B - A )

Portanto, sendo n ( A ) = x + y e n ( B ) = y + z, temos

n ( A ) + n ( A ) - n ( A B ) = ( x + y ) + ( y + z ) - y = x + y + z.

Como n ( A ∪ B ) = x + y + z, então n ( A ∪ B ) = n ( A ) + n ( B ) - n ( A B ).

Exemplo 1:

Uma pesquisa em uma turma de graduação em Computação, de 60 alunos, revelou que 40 deles pretendem fazer Especialização e 30 deles pretendem fazer Mestrado.

Supondo que todo aluno da turma queira fazer Mestrado ou Especialização, decida quantos alunos esperam fazer Especialização e Mestrado.

Solução:
Vamos considerar os seguintes conjuntos:

M = { alunos que querem fazer Mestrado }
E = { alunos que querem fazer Especialização }

Então, n ( M ) = 30, n ( E ) = 40 e n ( B ∪ A ) = 60. Logo, temos

n ( M E ) = n ( E ) + n ( M ) - n ( M ∪ E ) = 40 + 30 - 60 = 10.

Portanto, 10 alunos nesta turma esperam fazer Mestrado e Especialização. O problema pode ser representado pelo diagrama.

Uma outra solução seria usarmos uma variável. Como não sabemos quanto é n ( M E ), vamos escrever n ( M E ) = x. Agora completamos o diagrma.

Temos n ( M ) = 30, logo,

n ( M - E ) = 30 - x .

Temos n ( E ) = 40; assim,

n ( E - M ) = 40 - x .

Somando o número de elementos das partes de M ∪ E, obtemos:

n ( M ∪ E ) = 60 = ( 30 - x ) + x + ( 40 - x ) = 70 - x, que resulta em x = 10. Isto é, n ( M E ) = 10.

Substituindo o valor obtido de x do diagrama acima, obtemos o número de elementos de todas as partes de M ∪ E.

Exemplo 2:

Um pesquisa foi realizada com pessoas que lêem revistas semanais. Entrevistando 200 pessoas, descobriu-se o seguinte:

85 pessoas compram a revisa A,
75 pessoas compram a revista B,
65 pessoas compram a revista C,
30 pessoas compram as revistas A e B,
25 pessoas compram as revistas A e C,
20 pessoas compram as revistas B e C,
10 pessoas compram as três revistas.

Com base nestes dados, responda ao seguinte:

a) Quantas pessoas compram pelo menos uma das revistas?
b) Quantas pessoas não compram nenhuma das três revistas?
c) Quantas pessoas compram exatamente uma das revistas?
d) Quantas pessoas compram exatamente duas das revistas?

Solução:

Seja U o conjunto das pessoas que foram entrevistadas.

Sejam

A = { x U | x compra a revista A }
B = { x U | x compra a revista B }
C = { x U | x compra a revista C }

O diagrama abaixo representa a situação.

Comecemos com a região que representa o conjunto das pessoas que compram as três revistas. Este é o conjunto A B C e tem 10 elementos.

Em seguida, consideramos as interseções de dois conjuntos. Um total de 30 pessoas compra as revistas A e B, isto é, n ( A B ) = 30. Portanto,

30 - 10 = 20 compram apenas as revistas A e B.

Analogamente, n ( A C ) = 25. Portanto, 25 - 10 = 15 pessoas compram apenas as revistas A e C.

Por último, n ( B C ) = 20. Portanto, 20 - 10 = 10 pessoas compram apenas as revistas B e C.

Com as informações obtidas até agora, temos o diagrama da figura abaixo.

O próximo passo é determinar o número de pessoas que compram apenas a revista A, apenas a revista B ou apenas a revista C.

Vejamos, n ( A ) = 85. Subtraindo o número dos que compram outras revistas, temos:

85 - 10 - 20 - 15 = 40

Portanto, 40 pessoas compram apenas a revista A.

Analogamente, n ( B ) = 75. Logo,

75 - 10 - 20 - 10 = 35 pessoas compram apenas a revista B.

Finalmente n ( C ) = 65. Portanto,

65 - 15 - 10 - 10 = 30 pessoas compram apenas a revista C.

Agora podemos acabar de preencher o diagrama e passar a responder as perguntas:

a) Somando o número de elementos de todas as partes de A ∪ B ∪ C, obtemos

n ( A ∪ B ∪ C ) = 30 + 40 + 20 + 15 + 10 +35 + 10 = 160

Portanto, 160 pessoas compram pelo menos uma das três revistas.

b) Como n ( U ) = 200, então

n ( U ) - n ( A ∪ B ∪ C ) = 200 - 160 = 40 pessoas não compram nenhuma das três revistas.

c) Temos que 40 pessoas compram apenas revista A, 35 compram apenas revistas B e 30 compram apenas revista C. Portanto,

40 + 35 + 30 = 105 pessoas compram apenas uma das revistas.

d) Temos que 20 pessoas compram revistas A e B, mas não C; 15 pessoas compram revistas A e C, mas não B; 10 pessoas compram revistas B e C, mas não A. Portanto,

10 + 15 + 20 = 45 pessoas compram exatamente duas revistas.

Vimos então que:

n ( A ∪ B ) = n ( A ) + n ( B ) - n ( A )

Em particular, se A e B são disjuntos, então n ( A B ) = 0 e logo,

n ( A ∪ B ) = n ( A ) + n ( B ) - n ( A ) = n ( A ) + n ( B )

Princípio da inclusão e exclusão para três conjuntos

Pensando como nos exemplos anteriores, podemos provar o Princípio da inclusão-exclusão para 3 conjuntos:

Dados 3 conjuntos A, B e C, vale que:

n ( A ∪ B ∪ C ) = n ( A ) + n ( B ) + n ( C ) - n ( A B ) - n ( A C ) - n ( B C ) + n ( A B C )

Agora vamos realizar um exemplo trabalhando com variáveis

Exemplo:

O técnico da seleção brasileira de futebol convocou 22 jogadores para um amistoso. Destes, 2 são goleiros, 10 podem jogar na defesa, 10 podem jogar no meio-de-campo e 9 podem jogar no ataque.

Sabe-se também que 4 jogadores podem jogar na defesa e no meio, 5 jogadores podem jogar no meio ou no ataque e apenas 1 jogardor pode jogar da defesa e no ataque.

Os goleiros só podem jogar no gol. Perguntas:

a) Quantos jogadores são tão versáteis que podem jogar na defesa, no meio e no ataque?
b) Quantos podem jogar apenas da defesa?
c) Quantos podem jogar apenas no ataque?
d) Quantos podem jogar no ataque ou no meio, mas nunca na defesa?

Solução:

Seja U o conjunto dos 22 jogadores convocados. Representamos este problema por quatro regiões que correspondem ao conjunto D, A, M e G, dos jogadores que podem jogar na defesa, no ataque, no meio e os goleiros, respectivamente.

A região G é disjunta das demais, isto é, G ( D ∪ A ∪ M ) = . Temos que n ( G ) = 2, portanto:

n ( D ∪ A ∪ M ) = 22 - 2 = 20

Para determinar o número de elementos de cada região, vamos, como no exemplo anterior, começar com a intereseção dos três conjuntos. Contudo, não foi dado o número de elementos da intereseção dos três conjuntos.

Uma solução é usar uma variável x para representar n ( D A M ) e determinar o número de elementos das outras regiões em função desta variável.

O número de elementos das interseções de cada par de conjunto é n ( D M ) = 4, n ( D A ) = 1 e n ( M A ) = 5. Com esta informação, chegamos ao diagrama da figura abaixo.

Para completar o diagrama, calculamos, em função da variável x, o número de jogadores que jogam apenas na defesa, apenas no meio e apenas no ataque.

Temos que n ( D ) = 10. O número de jogadores que atuam apenas na defesa é

10 - ( 1 - x ) - ( 4 - x ) - x = 5 + x

Como n ( M ) = 10, o número de jogadores que atuam apenas no meio é

10 - ( 5 - x ) - ( 4 - x ) - x = 1 + x

Como n ( A ) = 9, o número de jogadores que atuam apenas no ataque é

9 - ( 1 - x ) - ( 5 - x ) - x = 3 + x

Com esta informação, completamos o diagrama.

Somando as partes de D ∪ M ∪ A, obtemos:

20 = n ( D ∪ M ∪ A )
20 = ( 5 + x ) + ( 3 + x ) + ( 1 + x ) + ( 4 - x ) + ( 1 - x ) + ( 5 - x ) + x
20 = 19 + x
x = 1

Substituindo o valor de x, obtemos finalmente o diagrama a seguir.
Com ele podemos responder facilmente as questões propostas.

a) Apenas um jogador pode jogar na defesa, no meio e no ataque.

b) Seis jogadores podem jogar apenas na defesa.

c) Quatro jogadores podem jogar apenas no ataque.

d) Os jogadores que não podem jogar na defesa são em número de 4 + 4 + 2 = 10

Princípio da inclusão e exclusão para quatro conjuntos

?????

4. Questões de AD´s e AP´s do Cederj

01. (Cederj 2006/1 - AD01) - Mostre a seguinte igualdade usando as propriedades de conjunto. (Observação. não verifique por diagrama de Venn).

( A - B ) ∪ ( B - A ) = ( A ∪ B ) - ( A B )


Resposta:

Prova:

02. (Cederj 2006/2 - AD01) - Quantos inteiros, entre 1 e 1000 inclusive, são divisíveis por pelo menos um dos números 2, 3 e 10? Justifique.

Resposta:

Sejam A = { x | 1 x 1000 e x é divisível por 2 } =
{ x | 1 x 1000, x = 2k para algum k },
B = { x | 1 x 1000 e x é divisível por 3 } =
{ x | 1 x 1000, x = 3k para algum k } e
C = { x | 1 x 1000 e x é divisível por 10 } =
{ x | 1 x 1000, x = 10k para algum k }

O conjunto dos números naturais entre 1 e 1000 que é divisível por pelo menos um dos números 2, 3 e 10 é o conjunto A ∪ B ∪ C. Precisamos portanto determinar n ( A ∪ B ∪ C ).

Pelo princípio de inclusão e exclusão, sabemos que:

n ( A ∪ B ∪ C ) = n ( A ) + n ( B ) + n ( C ) - n ( A B ) - n ( A C ) - n ( B C ) + n ( A B C )

Calcularemos o número de elementos de cada conjunto:

Como os elementos de A são da forma 2k e atendem a condição 1 2k 1000 para algum k , temos k . Logo, o primeiro elemento de A corresponde a k = 1 e o último a k = 500, portanto n ( A ) = 500. De forma análoga obtemos que o primeiro elemento de B corresponde a k = 1 e o último a k = 333, logo n ( B ) = 333.

Como o primeiro elemento de C corresponde a k = 1 e o último a k = 100, temos n ( C ) = 100.

Os demais conjuntos são:


A B = { x | 1 x 1000 e x é divisível por 2 e 3 } = { x | 1 x 1000, x = 6k para algum k } = { x | x = 6k, k , k } =
{ 6.1, ..., 6.166 }. Logo, n ( A B ) = 166.


A C = { x | 1 x 1000 e x é divisível por 2 e 10 } = { x | 1 x 1000, x = 10k para algum k } = { x | x = 10k, k , k } =
{ 10.1, ..., 10.100 }. Logo, n ( A B ) = 100.


B C = { x | 1 x 1000 e x é divisível por 3 e 10 } = { x | 1 x 1000, x = 30k para algum k } = { x | x = 30k, k , k } =
{ 30.1, ..., 30.33 }. Logo, n ( A B ) = 33.


A B C = { x | 1 x 1000 e x é divisível por 2, 3 e 10 } = { x | 1 x 1000, x = 30k para algum k } = { x | x = 30k, k , k } =
{ 30.1, ..., 30.33 }. Logo, n ( A B ) = 33.

Logo,

n ( A ∪ B ∪ C ) = 500 + 333 + 100 - 166 - 100 - 33 + 33 = 667

5. Bibliografia

Apostila de Matemática Discreta Volume 1 Cederj